Chapter 1.3- Shifting, Reflecting, and Stretching Graphs

Chapter 1.3

Chapter 1.3 explains how vertical and horizontal shifting, reflecting, and stretching graphs is possible.

Parent functions are basic functions that can be graphed very easily. Some common parent functions include identity functions, absolute value functions, and square root functions.

Parent functions can have transformations occur to them, and in result produce daughter functions that are similar to the parent functions except that they are transformed or altered in specific way. These transformations include:

Vertical and Horizontal Shifting

Vertical shifting to a parent function can cause the function to either move up or down the vertical axis depending on if the number added to the function is positive or negative. Positive number = graph moves upward that many units. Negative number = graph moves down that many units on the y axis

f(x)= x² is the parent function (red graph)

And f(x) = x²+3 is the daughter function (blue graph) that is shifted 3 units up on the y axis since 3 is a positive number.

If the parent function again is f(x)= x²

And f(x) =x² – 2 a transformed version, the original function on a graph will be shifted two units downward on the y axis

Horizontal shifting is when the parent function is transformed by shifting to either the left or the right along the x axis. This can occur when a number is either added or subtracted directly from x. When a positive number is added to x, the function shifts to the left. When a negative number is added to x, the function is shifted to the right.

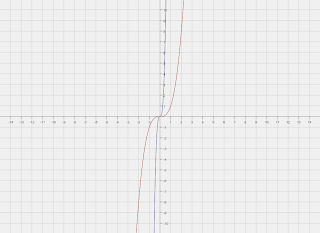
When the original function is

f(x)=x (red graph) and then it is transformed by adding 2, f(x)=(x=2) (blue graph) the new function is shifted to the left by two units on the x axis.

When the same parent function, f(x)=x, is altered by subtracting 4, f(x)=x-4, the original function is shifted to the right 4 units on the x axis.

Overview:

1. Vertical shift c units upward: h(x) = f(x) + c

2. Vertical shift c units downward: h(x) = f(x) - c

3. Horizontal shift c units to the right: h(x) = f(x - c)

4. Horizontal shift c units to left: h(x) = f(x + c)

Reflecting Graphs

A Reflection can be considered a mirror image of the parent function and is reflected either in the x-axis or in the y-axis.

Reflections in the coordinate axes of the graph of y = f(x) are represented as follows:
1. reflection in the x-axis: h(x)= -f(x)
2. reflection in the y-axis: h(x)= f(-x)

If the parent function is

(red)

Then the reflection in the x-axis of this function,

(blue) are both graphed like:

If the reflection in the y-axis were found from the same parent function,

, then the new equation would be f(x)=

and the graph would look like:

***Side Note***

Rigid transformations include horizontal shifts, vertical shifts, and reflections. They are rigid transformations because the basic shape of the graph goes unchanged, only the position on the graph is altered in the xy plane.

Nonrigid transformations on the other hand do change the basic shape of a function (distortion). These type of transformations include vertical and horizontal stretches which will be discussed below.

Stretching Graphs

A vertical stretch is an alteration or distortion to a parent function by making the function skinner and lengthier.

A vertical compress is an alteration or distortion to a parent function by making the function wider.

A nonrigid transformation of the graph of y = f(x) is represented by y = cf(x)

a vertical stretch occurs if c > 1

a vertical compress occurs if 0 < c < 1

If the parent function is:

(red graph)

A vertical stretch can be: f ( x ) = 4 |x| (blue graph) , so the graph is:

If the parent function is:

A vertical shrink can be: f ( x ) = (1/2) |x| , so the graph looks like:

For horizontal stretches, the nonrigid transformation of the graph of y = f(x) is represented by            y = f(cx).
             a horizontal compress is when c > 1
             a horizontal stretch is when 0 > c >1

If the parent function is: