In this section we will discuss summation notation.
Summation notation is also known as sigma notation because it involves the use of the upper case Greek letter sigma, written as
 .
.Definition of Summation Notation
i is the index of summation
n is the upper limit of summation
1 is the lower limit of summation
Example:
Properties of Sums
Series
An infinite series or simply a series involves the sum of the terms of an infinite sequence.
Definition of a series
2. The sum of the first n terms of the sequence is calls a finite series or the nth partial sum and is denoted by.

Example



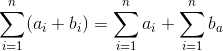



No comments:
Post a Comment