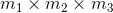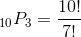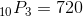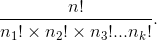9.5 The Binomial Theorem

The Binomial Theorem is used when finding the coefficients of expanded binomials.

The Binomial Theorem in the expansion of  :



The coefficient of can be found using:

Another way to write: is.


Example : Find the binomial coefficients of :

Step 1: Plug in to formula=

Step 2: Solve====


Example: Find the binomial coefficients of :

Step 1: Plug into formula =

Step 2: Solve ====


Pascal's Triangle:

Another way to find binomial coefficients is through Pascal's Triangle.

In the triangle, each number is found by adding together the two numbers above it. Example: 3+3=6 These numbers are the same as the coefficients of expanded binomials:

Example: Expand the binomial 

    

    Step 1: Find Coefficients

            The coefficients from the 4^th row of Pascal’s Triangle are 1,4,6,4,1

   

    Step 2: Expand

   

    Step 3: Simplify 

When expanding binomials that have subtraction signs instead of addition you alternate the signs in front of each coefficient.

   Example: Expand the binomial 

   The coefficients are the same but the signs alternate: 

9.6 Counting Principles

Simple Counting Problems

• Counting the number of ways an event can occur is important, because it necessary in order to understand probability. 
• The easiest way to solve simple counting problems is to list each possible way that an event can occur. 

The Fundamental Counting Principle 

Some events can occur in so many different ways that it is not feasible to write out the entire list. In such cases, you must use formulas and counting principles. The most important of these is the Fundamental Counting Principle.

Fundamental Counting Principle 

• Let E₁ and E₂ be two events. The first event E₁ can occur in m₁ different ways. After E₁ has occurred, E₂ can occur in m₂ different ways. The number of ways that the two events can occur is 
  
• The Fundamental Counting Principle can be extended to three or more events. For instance, the number of ways that three events E₁, E₂, and E₃ can occur is 
  
   

Example: Using the Fundamental Counting Principle 

At an ice cream store, there are 11 ice cream flavors. There are 7 options for toppings. Additionally, there are 3 colors of spoons available. How many total choices are there?

Total choices =

Thus, there are 231 total choices. 

Permutations 

You can use the Fundamental Counting Principle to determine the number of ways that n elements can be arranged in order. An ordering of n elements is called a permutation of the elements.

Definition of Permutation

• A permutation of n different elements is an ordering of the elements such that one element is first, one is second, one is third, and so on.   

Number of Permutations of n Elements 

• The number of permutations of n elements is

• In other words, there are n! different ways that n elements can be ordered. 

                                                                                 

Example: Finding the Number of Permutations of n Elements 

How many permutations are possible for the letters S, T, A, and R?

Consider the following reasoning:

First position: Any of the four letters
Second position: Any of the remaining three letters
Third position: Either of the remaining two letters
Fourth position: The one remaining letter

The total number of permutations of the six letters is

Occasionally, you are interested in ordering a subset of a collection of elements rather than the entire collection. For example, you might want to choose (and order) r elements out of a collection of n elements. Such an ordering is called a permutation of n elements taken r at a time.

Permutations of n Elements Taken r at a Time

• The number of permutations of n elements taken r at a time is 
  

Example: Permutations of n Elements Taken r at a Time

Ten people are competing in a swim meet. In how many different ways can these people come in first, second, and third. (Assume that there are no ties.)

In this problem, you are trying to find the number of permutations of ten people taken three at a time. One can successfully accomplish this by using the formula for the number of permutations of n elements taken r at a time.

Step 1:

Step 2:

Step 3: 

Step 4: 

There are 720 different ways the ten people can come in first, second, and third.

Distinguishable Permutations 

Suppose a set of n objects has n₁ of one kind of object, n₂ of a second kind, n₃ of a third kind, and so on, with 

The number of distinguishable permutations of the n objects is 

  

Combinations

Now, we will discuss a method of selecting subsets of a larger set in which order is not important. Such subsets are called combinations of n elements taken r at a time.

Combinations of n Elements Taken r at a Time

The number of combinations of n elements taken r at a time is

  




Example: Combinations of n Elements Taken r at a Time

Seven slips of paper with the letters N, G, S, F, R, T, C written on them are put into a hat. The letters stand for Nicholas, George, Stephanie, Felicia, Rose, Tessa, and Carly, respectively, and they represent seven people who have been entered to win a brand new flat screen television. Three winners will be chosen. In how many different ways can three letters be chosen from the letters on the slips of paper if the order of the three letters is not important?

In this problem, you are trying to find the number of combinations of seven people taken three at a time. One can successfully accomplish this by using the formula for the number of combinations of n elements taken r at a time.

Step 1:

Step 2:

Step 3: 

Step 4:

There are 35 combinations.