The art of calculus serves two primary purposes. These are finding the slope of a point on a curve, and finding the area under a curve. The ability to take these measurements is essential to modern engineering, physics, and economics. The first of these two abilities will be covered here. This blog post contains the basics of tangent lines and derivatives.
Warning:
Calculus may seem like a fun tool, but it is nothing to take lightly. Its capacity for calculation is great, but so is its ability to destroy. Only read this post if you are willing to risk being corrupted by the immense power you are about to wield.
The idea behind derivatives is to find the slope of a function at a given input. This means it is finding the slope at a single point. The slope at any point can be easily figured with algebra if the function is a straight line, but if it is anything else then calculus becomes necessary.
The way to find the slope of a point on a curved line is to find the slope of its tangent line. A tangent line is a line that intersects that part of the function at exactly one spot. It can cross the path of the function elsewhere, but it can only touch the curve you are evaluating once. The slope of this line will be the slope of the function at that particular point.
Derivatives can be used to find the slope of these tangent lines. This is achieved by first using the difference quotient.
The difference quotient is the formula for the function that will tell you the slope of the line between f(x) and f(x+h). To find the slope at f(x) for any point x, one must first plug the f(x) into the difference quotient formula. Let's do this for f(x)=x^2
This simplified function now tells us the slope between the points f(x) and f(x+h) in the function f(x)=x^2 for any value x and h. The way to use this information to find the slope at f(x) is to apply the concept of limits. Since h is the difference in x values between the two points, h must be made as small as possible without being 0 to find the slope of the tangent line of the single point f(x). This can be done by taking the limit of the simplified difference quotient as it approaches 0.
The resulting limit is known as the derivative of f(x). For any x value that is put into this derivative, the resulting value will be the slope at f(x). For example, this means where x = 0, the slope of the function is equal to 2(0), or 0. Where x=2, the slope of the function is 2(2), or 4.
This same process can be used to find the slope of any point on any graph. Just find the derivative by taking the difference quotient as h approaches 0, and plug in any x value to find the slope at that exact point.
Ian Hoeck




.gif)
.gif)
.gif)
.png)





.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)


.gif)
.gif)

.gif)
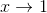.gif)

.gif)
.gif)






.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)


.gif)
.gif)
.gif)
.gif)