5.3-Solving Trigonometric Equations

The goal of solving trigonometric equations is to isolate the trigonometric function involved in the equation, this can be done using standard algebraic techniques.

Solving a basic trig equation

2sin(x)-1=0                        Original equation

2sin(x)=1                        Add one to each side

sin(x)=1/2                        Divide each side by 2

Use the unit circle or sine wave to find the solutions to this equation

According to the unit circle and sine wave

Therefore  and  are the two solutions in the interval ⊏0,2∏).

 If you want to express all possible solutions for this trig equation add 2n∏ (because the period is 2∏)  to the end of each solution. For this particular equation, there are infinitely many solutions.  (n is an integer)

Factoring Trig Equations

By taking out the cot(x), you can then use the zero product property.

The solutions x=∏/2 and x=(3∏)/2 come from the equation cot(x)=0

This equation needs to be simplified further

 Add 2 to both sides and then take the square root of both sides.

*Watch out for equations that can have no solution because their solution is outside the range of the function.

The real solutions to this equation is: 

*Remember, the period of cot is ∏, not 2∏. If you want to express all possible solutions for this trig equation add n∏ to the end of each solution. For this particular equation, there are infinitely many solutions.  (n is an integer)

*It would be redundant for this to be the solution:(The first equation is the simplified solution it is the only solution necessary for the final answer.)

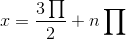
 Sum and Difference of Cubes

-Sometimes you will need to use the sum or difference formula in order to solve trig equations. It is helpful to remember the phrase: Same, opposite, always positive (S.O.A.P) when factoring.

Posted by Liz.