Simplifying, you get
Again, simplify:
Examples:
Solving a Double-Angle Equation
1) Begin by using a double-angle formula for cosine:
2) Next, factor.
3) Set the factors equal to zero and simplify.
4) Solve for x on the given interval.
Using Double-Angle Formulas in Sketching Graphs
1) First, factor out a 2.
2) Then, you can substitute using a double-angle formula.
Using this information, we can sketch the graph:
Evaluating Functions Involving Double Angles

1) From the given information, you can draw a triangle like this:
2) Next, you use the double-angle formula, substitute in the known values, and simplify.

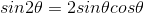






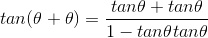




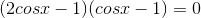

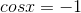













No comments:
Post a Comment