 |
Consider 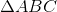 and and .gif) . . |
Using sum and difference formulas: In this section, we study the use of several new trigonometric identities and formulas.
Sum and difference formulas can be used to find the exact values of trigonometric functions involving sums or differences of special angles (angles whose sines, cosines, and tangents can be found on the unit circle).
Deriving the sum and difference formulas:
.gif)
AND
Substituting those values in, we find that...
we are able to divide out AD and conclude that
THIS is our first sum and difference formula.
Assuming they are derived through a similar process, we must also know these formulas:
Using these formulas and our knowledge of the quotient identities, we can also derive the sum and difference formulas for the tangent function. We know that:
using the formulas we just derived, we can say that:
To get the difference formula for the tangent function, you simply use
and use the same process, to yield a similar equation, but with different signs.
Example:
Find the exact value of the sine, cosine and tangent of an angle with the measure:
EVALUATING SINE
EVALUATING COSINE
EVALUATING TANGENT
Sum and difference formulas can also be used to prove trigonometric identities, as in this example:
Prove the confuction identity:
Using the formula for cos(x-y), you have
You can also use these identities to solve trigonometric equations, as in this example:
Find all solutions of
on the interval
Using sum and difference formulas, rewrite the equation as
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
No comments:
Post a Comment