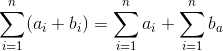Simple Counting Problems
- Counting the number of ways an event can occur is important, because it necessary in order to understand probability.
- The easiest way to solve simple counting problems is to list each possible way that an event can occur.
The Fundamental Counting Principle
Some events can occur in so many different ways that it is not feasible to write out the entire list. In such cases, you must use formulas and counting principles. The most important of these is the Fundamental Counting Principle.Fundamental Counting Principle
- Let E1 and E2 be two events. The first event E1 can occur in m1 different ways. After E1 has occurred, E2 can occur in m2 different ways. The number of ways that the two events can occur is
- The Fundamental Counting Principle can be extended to three or more events. For instance, the number of ways that three events E1, E2, and E3 can occur is
At an ice cream store, there are 11 ice cream flavors. There are 7 options for toppings. Additionally, there are 3 colors of spoons available. How many total choices are there?
Total choices =
Thus, there are 231 total choices.
Permutations
You can use the Fundamental Counting Principle to determine the number of ways that n elements can be arranged in order. An ordering of n elements is called a permutation of the elements.
Definition of Permutation
- A permutation of n different elements is an ordering of the elements such that one element is first, one is second, one is third, and so on.
Number of Permutations of n Elements
- The number of permutations of n elements is
- In other words, there are n! different ways that n elements can be ordered.
How many permutations are possible for the letters S, T, A, and R?
Consider the following reasoning:
First position: Any of the four letters
Second position: Any of the remaining three letters
Third position: Either of the remaining two letters
Fourth position: The one remaining letter
The total number of permutations of the six letters is
Occasionally, you are interested in ordering a subset of a collection of elements rather than the entire collection. For example, you might want to choose (and order) r elements out of a collection of n elements. Such an ordering is called a permutation of n elements taken r at a time.
Permutations of n Elements Taken r at a Time
Example: Permutations of n Elements Taken r at a Time
Ten people are competing in a swim meet. In how many different ways can these people come in first, second, and third. (Assume that there are no ties.)
In this problem, you are trying to find the number of permutations of ten people taken three at a time. One can successfully accomplish this by using the formula for the number of permutations of n elements taken r at a time.
Step 1:
Step 2:
Step 4:
There are 720 different ways the ten people can come in first, second, and third.
Distinguishable Permutations
Suppose a set of n objects has n1 of one kind of object, n2 of a second kind, n3 of a third kind, and so on, with
The number of distinguishable permutations of the n objects is
Combinations
Now, we will discuss a method of selecting subsets of a larger set in which order is not important. Such subsets are called combinations of n elements taken r at a time.Combinations of n Elements Taken r at a Time
The number of combinations of n elements taken r at a time isExample: Combinations of n Elements Taken r at a Time
Seven slips of paper with the letters N, G, S, F, R, T, C written on them are put into a hat. The letters stand for Nicholas, George, Stephanie, Felicia, Rose, Tessa, and Carly, respectively, and they represent seven people who have been entered to win a brand new flat screen television. Three winners will be chosen. In how many different ways can three letters be chosen from the letters on the slips of paper if the order of the three letters is not important?
In this problem, you are trying to find the number of combinations of seven people taken three at a time. One can successfully accomplish this by using the formula for the number of combinations of n elements taken r at a time.
Step 1:
Step 2:
Step 3:
Step 4:
There are 35 combinations.

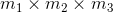







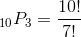

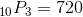

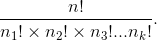





.gif)
.gif)
.gif)
.gif)
.gif)