Complex numbers are defined as the addition of both real and imaginary numbers.
REAL numbers include rational numbers, irrational numbers, integers, whole numbers, and natural numbers.
IMAGINARY numbers include the imaginary unit, i. i can be defined as:
Complex numbers are written in standard form a+bi where a is the real part of the complex number and bi is the imaginary part.
Operations with Complex Numbers
ADDITION: (a+bi) + (c+di) = (a+c) + (b+d)i
Ex: (4+3i) + (5+i) = 4 + 3i + 5 + i Remove parenthesis
= 4 + 5 + 3i + i Group like terms
= (4+5) + (3+1)i
= 9 + 4i Write in standard form
SUBTRACTION: (a+bi) -(c+di) = (a-c) + (b-d)i
Ex: (2-i) - (7+2i) = 2 - i - 7 - 2i Remove parentheses
= 2 - 7 - i - 2i Group like terms
= (2-7) - (1+2)i
= -5-3i Write in standard form
MULTIPLICATION: To multiply complex numbers, use the FOIL system (first, outside, inside, last) and the distributive property.
Ex: (3+2i)(6+i) = 18 + 3i + 12i + 2
Multiply out using FOIL= 18 + 15i + 2
Combine like terms,= -1= 18 + 2(-1) + 15i
= 16+15i
DIVISION: In order to divide complex numbers, you must multiply the numerator and denominator by the conjugate of the denominator. If the denominator is a+bi, the conjugate would be a-bi.
Ex:
Applications
PLOTTING COMPLEX NUMBERS: In the complex plane, you must remember this: the imaginary axis is the vertical (y) axis and the real axis is the horizontal (x) axis. So this would mean that the point representing the complex number a+bi would be (a,b).
Ex: Plot the complex number 2+3i
To plot this point: move 2 units to the right on the real axis and move 3 units up on the imaginary axis. The graph would look like this:
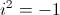
No comments:
Post a Comment