Polynomial functions
- The function is called a polynomial function of x with degree n.
- Polynomial functions are classified by degree.
- It has a degree of 0.
- It has a degree of 1.
- The type of polynomial function discussed in this section is the quadratic function.
Quadratic Functions
- Let a, b, and c be real numbers with

- The graph of a quadratic function is a special type of U shaped curve called a parabola.All parabolas are symmetric with respect to a line called the axis of symmetry.
- The point where the axis intersects the parabola is the vertex of the parabola.
- If the leading coefficient a is positive, the graph is a parabola that opens upward. If the leading coefficient a is negative, the graph is a parabola that opens downward.
- The simplest type of quadratic is

- In the graph a > 0, the vertex is the minnimum point on the graph; and if a < 0, the vertex is the maximum point on the graph.
Vertex = (-2, -9)
- How to complete the square










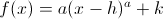









No comments:
Post a Comment