2.3 Real Zeroes of Polynomial Functions

This section contains information on long division of polynomials, synthetic division, the remainder theorem and the rational zero test.

Long Division of Polynomials

One way to divide polynomials by other polynomials is to use long division.

Example: Divide by x+3

After dividing, we can tell that the remainder is zero because there are no numbers that are left over. Since we know (x+3)(2x+4)=we can find the x intercepts of the graph:

(x+3) (2x+4)

x+3=0   2x+4=0

x=-3      x=-4/2

              x=-2

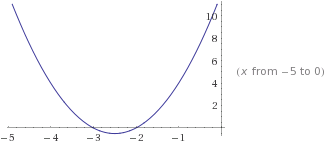
The x intercepts are located on the graph at x=-3 and x=-2.

When dividing polynomials, sometimes there will be a remainder that is left over.

Example: Divide by x+2

In this equation, the remainder is -23. The answer to this problem can be written as:

Synthetic Division

Synthetic division is another method you can use when finding the zeroes of polynomials.

Example: Divide  by x+3

Setting it up: 1. The divisor is x+3 which means that x=-3. The -3 is placed to the left.

                    2. The coefficients of the dividend are 2, 10 and 12. These numbers are placed in order to the                            right of the -3.

Step 1: Bring down the 2

Step 2: Multiply the 2 by -3= -6

Step 3: Add 10 + (-6) = 4

Step 4: Multiply the 4 by -3= -12

Step 5: Add 12 + (-12) = 0

When using synthetic division, multiply the terms going diagonally and then add the terms vertically. x+3 is a factor of the equation because it has no remainder. If there was a remainder, then x+3 would not be a factor.

Example: Divide  by x+5

Since the remainder is 12, x+5 is not a factor.

The Remainder Theorem

The remainder theorem: f(k)=r

If a polynomial f(x) is divided by x-k

Example: Divide  by x+6

Using the remainder theorem we know F(-6) =-65

This tells us that (-6, -65) is a point on the graph of f which can be seen below.

Rational Zero Test

If this polynomial

Has integer coefficients, every rational zero of f can be found using this equation:

p= factors of the constant term 

q= factors of the leading coefficient

Example:  Find all possible rational zeroes of 
p= factors of 6
q= factors of 5

*These are only the possible rational zeroes. They can be tested individually using synthetic division to determine if they are actual rational zeroes.
Example: Test x=-1 to see if it is a rational zero

Since there is a remainder of -4, x=-1 is not a rational zero.