3.1 Exponential Functions and Their Graphs

3.1 Exponential Functions and Their Graphs:

Exponential Functions-

The exponential function of with base is denoted as

                                        

where , ,and is any real number

If you are wondering why , it is because it yields a constant function not an exponential function. 1 raised to any power will always equal 1.

Graphs of Exponential Functions-

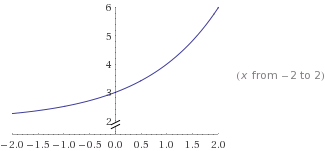
Below is the graph of 

The basic characteristics of this graph are:

• Domain:    
• Range: 
• Intercepts: 
• X-axis is horizontal asymptote as
• Increasing
• Continuous

Comparatively the graph of 

It has all of the same basic characteristics as however, the graph of   increases more rapidly.

Transformations of Exponential Functions
The form:

shows graph transformations more clearly.

effects how quickly the graph will either increase or decrease
effects up and down shifts in the graph
effects left and right shifts in the graph
effects reflections over of the y-axis
Reflections over the x-axis occur if the whole function is multiplied by a negative for example:

We have already seen how effects the graphs so let's begin with a shift up or down.

This graph is the same as  shifted but up 2 units
The only basic differences are that the y-intercept becomes and the horizontal asymptote becomes y=2

This graph is the same a shifted but shifted right 2
The only difference is the y-intercept

This graph is the same as translated across the x-axis
The function is now decreasing and has the y-intercept of

When the graph is translated across the y-axis and becomes decreasing
Note: Translations in the y-axis also can occur when



The Natural Base e
2.71828; e is the natural base
The natural exponential function is:

             

It is convenient choice for many applications.
For large values of x, e can be approximated by the expression  




Compound Interest
Compound Interest is a very common example of exponential growth where you earn interest on your interest
To calculate this use the equation:

A= Amount after interest
P= Initial Investment
r= Interest Rate
n= Amount of compounds a year
t= Years

Continuous Compounding occurs when n increases uncontrollably to the point where compounding is continuous. To solve for this type of compounding use the formula:

where e 2.71828