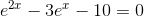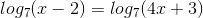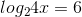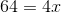3.4 Solving Exponential and Logarithmic Equations

There are 2 main methods you can use to solve equations involving exponential and logarithmic functions:

1) The “Key to Everything”

This states that:  if and only if 

This is the definition of a logarithm.

2) The One-to-One Property

This states that when  and :

 if and only if 

 if and only if 

This property works because exponential and logarithmic functions are one-to-one, meaning that for every x value, there is only one corresponding y value. In other words, they pass the vertical line test.

To illustrate the one-to-one property:

If , we can conclude that x=3.

It is also helpful to know the Inverse Properties of logarithms:

     We can show that this is true using the key to everything. 

     Rearranging the above equation, we find that:

 
     Again, the key to everything helps us prove this. Rearranging the equation, we see that:

Knowing all the other properties of logarithms, which can be found in the post on section 3.3, will also be very useful in solving such equations.

Examples:

Solving Exponential Equations  

1)  Solve for x.

     Given this equation, we can simplify the right side:

 
 
     Using the one-to-one property, we can then conclude that x=-5.

2)  Solve for x.

    Using the key to everything, we find that:

    Since a logarithm with a base of “e” is the same as a natural log, we simplify to:

    The answer can be written as x=ln3, which is approximately equal to 1.099.

Solving Exponential Equations in Quadratic Form

3) Solve .

    First, we substitute in  to get:

    Then, we factor and solve like a regular quadratic:

 and

    Next, we substitute again:

and

    Finally, using the key to everything, we find that: 

and *

    *HOWEVER: The solution x=ln(-2) is extraneous, because you cannot take the logarithm or the natural logarithm of a negative number. Therefore, the only real solution to this equation is x=ln5.

Solving Logarithmic Equations

4) Solve .

    Using the one-to-one property, we can simplify to: 

    Then, solve for x as you would normally.

5) Solve .

    We begin by simplifying:

    Then, using the key to everything, we find that:

    We can then solve for x.

3.2 Logarithmic Functions and Their Graphs

The logarithmic function f with base a is denoted as:
    f(x)=log_ax
where a>0, a≠1, and x is a real number.

The logarithmic function f(x)=log_ax is the inverse of the exponential function f(x)=a^x.

 These are the graphs for f(x)=log₁₀x (in blue) and f(x)=10^x (in red).

Notice that that the logarithmic graph is a transformation of the exponential graph.

       THE KEY TO EVERYTHING

With a logarithmic function, y=log_ax implies that a^y=x.

For example:
log₂4=2
implies that
2²=4.

When evaluating logarithmic functions, it is important to keep this in mind.

For example:
   log₅125=x
(We can solve for x by remembering The Key to Everything.)
   5^x=125
(125 is equal to 5³.)
   5^x=5³
(If 5 raised to the x power is equal to 5 raised to the 3^rd power, then...)
   x=3
(...x is equal to 3.)

       THE PROPERTIES OF LOGARITHMS

• log_a1=0 because a⁰=1
• log_aa=1 because a¹=a
• log_aa^x=x because a^x=a^x
• If log_ax=log_ay, then x=y.

The natural logarithmic function, similar to the natural exponential function, uses the number e as a base.
   For example: f(x)=log_ex
The natural logarithmic function is also rewritten in this way:
f(x)=ln x where ln denotes log_e.

The common logarithmic function is a logarithm with the base 10.
   For example: f(x)=log₁₀x
The common logarithmic function is also rewritten in this way:
f(x)=log x where log denotes log₁₀.

       GRAPHS OF LOGARITHMIC FUNCTIONS

Recall that the graph of the logarithmic function f(x)=log_ax is the inverse of the exponential function f(x)=a^x.
The graph of a logarithmic function is its corresponding exponential graph reflected across the line y=x.

These are the graphs for f(x)=log₁₀x (in blue), f(x)=10^x (in red), and f(x)=x (in orange).

In order to graph a logarithmic function, you should first graph its corresponding exponential function. Because they are inverses, you can find the corresponding exponential function by switching the x and y values.



Additionally, because they are inverses, the domain of one function is the range of the other, and the range of one function is the domain of the other.

   For example:
The domain (the possible x-values) of the function f(x)=log x is (0, ∞).
Therefore, the range (the possible y-values) of the function f(x)=10^x is (0, ∞).
The domain of the function f(x)=10^x is (-∞, ∞).
Therefore, the range of the function f(x)=log x is (-∞, ∞).